Bias vs Variance
The problem of “bias versus variance” represents the underlying tension when training a neural network. Bias refers to the discrepancy between the average prediction of a model and the actual value that the model is attempting to predict. Models with high bias tend to not fully adapt to the training data and oversimplify the model. On the other hand, Variance refers to the variability in the predictions of a model for a given data point, or the spread of the data. Models with high variance pay close attention to the training data and do not generalise well to unseen data.
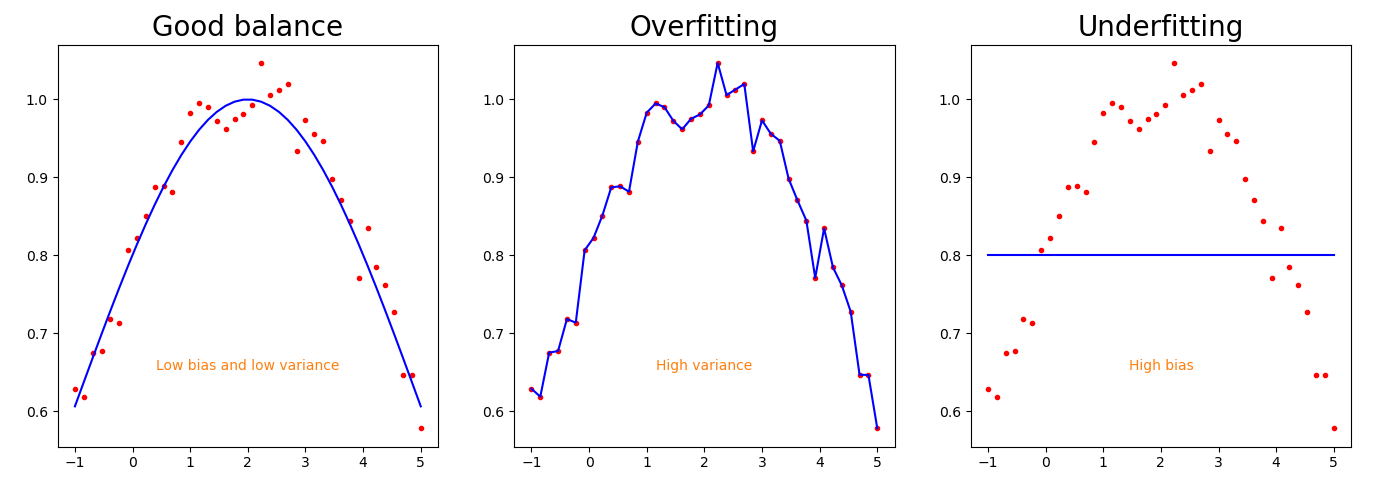
Fig. 1 Difference between bias and variance and their relation to overfitting and underfitting the training data.
Figure Fig. 1 depicts three different plots representing the approximation of three models. The red points are the data in the dataset and the blue line is the approximation of that specific model. The righthand plot shows a model with a high bias that underfits the data. The model represented in the middle plot, on the contrary, overfits the dataset by capturing the noise along with the underlying pattern in the data. The goal of the training process is to get a model like the one represented in the lefthand plot, with a good balance between bias and variance. A model capable of capturing the complex patterns in the dataset and, at the same time, capable of extrapolating its predictions to unseen data, not getting lost in the noise.
There are several ways of checking if our model is overfitting or underfitting the training data.
One of the most common practices is to split the dataset into three subsets: the training set, the development or validation set and the test set.
The training process involves multiple cycles, known as epochs, where the model goes through the entire training dataset.
After a predetermined number of iterations, the model performs a single forward pass on the validation dataset to assess its performance.
Once the training process concludes, the final model’s performance is evaluated using the test dataset.
Normally, for big datasets, the proportion of the training set is much bigger than the dev and test sets.
For example, the split proportions could be
We have seen how to detect if our model has a high variance or a high bias, but how can we correct these problems to obtain a balanced network? As a general rule of thumb, bigger networks or longer training can fix the problem of high bias but also increase the risk of high variance. On the other hand, more data and regularisation techniques can solve the problem of high variance but risk the high bias again. The most common regularization techniques to avoid overfitting (high variance) are explained in this post. Achieving a model with low bias and low variance is an iterative give-and-take problem.
To conclude this post, it is interesting mentioning another training strategy known as k-fold cross-validation.
This method involves dividing the training set into
Footnotes
-
Ng, Andrew Y. “Preventing” overfitting” of cross-validation data.” In ICML, vol. 97, pp. 245-253. 1997. ↩